Friends, this is such an interesting topic about the basic equations of electrodynamics, one of which can be written as induction and change our understanding of what happens in an electric circuit.

2.5.2. Maxwell's equation

JK Maxwell wrote down his ingenious equations in 1865. Maxwell's equations are the fundamental equations of electrodynamics that describe electromagnetic phenomena in any medium. They summarize the experimental and theoretical works of physicists of the first half of the 19th century. and, first of all, the research of M. Faraday. Maxwell formulated the basic laws of electrodynamics in the form of four equations, which will be presented in integral form, as in the simplest and clearest form.

Maxwell's first equation is based on the Biot-Savard-Laplace law and the concept of displacement current. In a conductor in which there is an alternating current, we select an arbitrary area bounded bythe Todi

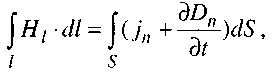(2.88)

where is the projection of the magnetic field intensity vector onto the direction of the tangent to the contour at this point, is the component of the conduction current density normal to the selected site, is the component of the electric induction vector normal to the site. The partial derivative dD / dt is used here to take into account the fact that D depends on both time and spatial coordinate. Bias current occurs only when D varies with time. This equation shows that the magnetic field is eddy and that it occurs regardless of the presence of permanent magnets. The emergence of the magnetic field is due to two factors: the movement of electric charges (conduction current) and the change in time of the electric field (displacement current).

The second equation reflects Faraday's law of electromagnetic induction:

EMF, as is known, is equal to the work of external forces on the movement of a unit charge, that is, we will have

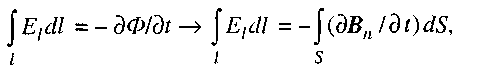(2.89)

where is the projection of the electric field intensity vector onto the direction of the tangent to the contour at a given point, is the component of the magnetic induction vector normal to the surface. It can be seen from this equation that, in addition to the electrostatic field, there is an electric field in nature, the source of which is an alternating magnetic field. Any change in the electric field leads to the appearance of a changing magnetic field, the lines of which are closed and cover the lines of the electric field (the first equation); any change in the magnetic field leads to the appearance of a changing electric field, the lines of which are closed and cover the lines of the magnetic field (the second equation).

Maxwell's third equation shows that the source of the electric field is electric charges:

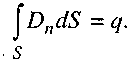
The left part of this equation is the flux of the electric field induction vector through a closed surface with an area of 5.

The fourth equation reflects the fact of the absence of magnetic charges. The total flux of the magnetic induction vector B through a closed surface of area S is zero:

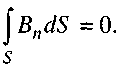
Maxwell's equations do not take into account the structure of matter and the interaction of the electromagnetic field with particles of matter. The influence of the environment on the electromagnetic field is given through its electrical conductivity, as well as dielectric ε and magnetic permeability. Therefore, three more equations, which are called material, should be added to Maxwell's equations:

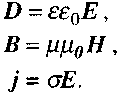
Maxwell's equations describe a huge range of phenomena (electrodynamics, optics, electrical engineering, radio engineering, astrophysics, plasma physics, etc.). Maxwell's theory not only explained already known facts, but also predicted new and important phenomena. Absolutely new in this theory was Maxwell's assumption about the magnetic fields of bias currents. On the basis of this assumption, Maxwell predicted the existence of electromagnetic waves, that is, a variable electromagnetic field that propagates in space at a certain speed. A theoretical study of the properties of electromagnetic waves later led Maxwell to create the electromagnetic theory of light. Later, the experimental group managed to obtain electromagnetic waves and conduct experiments that brilliantly confirmed the electromagnetic theory of light, and with it the entire theory of Maxwell.

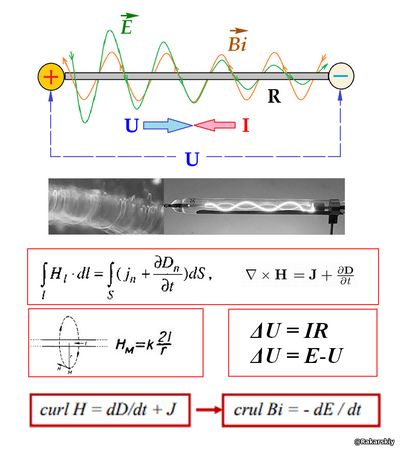
Maxwell's first equation for an electrical measurement system is expressed as the action of electromagnetic induction. We will replace the value of the current, which in the electrical measurement system is defined as a quantitative characteristic of electric charges moving in the conductor, with the value of the magnetic induction vector, which appears from the transformation of the EMF lines of force, which have a vector of action around a closed conductor between the poles of the source with a difference electric potentials..

crul H = dD/dt + J → crul Bi = - dE/dt

We can write the equation in a new form:

1) crul Bi = -dE /dt;

2 ) curl E = -dBm /dt;

3) div D = ρ;

4) div B = 0.

In the first equation of the new interpretation and the second one for electromagnetic induction, we introduce varieties: magnetic induction of the external magnetic field (Bm) and magnetic induction (Bi) around the conductor, from the EMF of the voltage source to which the conductor is connected. It is noteworthy that the magnetic induction from the external magnetic field does not have a direct reverse effect, the electromagnetic induction around the conductor has a reverse effect.
The reverse effect is manifested in the phenomenon of self-induction:

crul Bi = - dE / dt → crul E = - dBi / dt.

With Maxwell's first equation, physicists explain such a phenomenon as current displacement, which has many ambiguities, it is easier to explain that it can be a phenomenon of electromagnetic induction of reverse action:

2.5.1. Bias current

Let's return once again to the cause of the magnetic field. We talked about the fact that the cause of magnetism is the movement of electric charges. And what happens in the case of an open electric circuit, when the conductor itself is missing (the presence of a capacitor essentially means a circuit break)? How to explain the presence of alternating current in such a circuit?

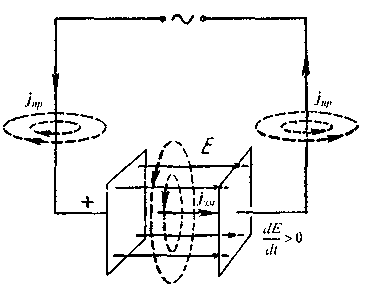
Fig. 2.39.

The outstanding physicist James Clark Maxwell (1831-1879) gave a physical explanation. This explanation is based on the concept of displacement currents, which are a kind of continuation of the usual conduction currents. Maxwell assumed that the magnetic field can be excited not only by an electric current, but also by an alternating electric field.

Let's find an expression for the bias current. To do this, consider the passage of an alternating current in a circle in which the capacitor is turned on (Fig. 2.39). The capacitor does not prevent the flow of alternating current and it can be assumed that the normal conduction current is shorted in the capacitor by the bias current

Charge on the plates of a flat capacitor

Then the bias current in the capacitor

and the bias current density

(2.81)

or, taking into account the relationship between the stress vectors E and the induction of the electric field (2.3),

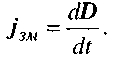(2.82)

Therefore, the displacement current density is equal to the rate of change with time of electric field induction. It follows from (2.81) that the vector is directed in the same direction as That is, if the capacitor is charged, the vectors have the same direction, if

vectors are opposite in direction.

Recall that in a dielectric, the induction vector of the electric field is related to the vectors of intensity and and polarization P by the ratio

Then the displacement current density in the dielectric consists of two terms:

(2.83)

The first term also occurs in a vacuum, the second term characterizes the displacement of electric charges in the dielectric, which causes the dielectric to heat up.

The most important property of the bias current is that it, like the conduction current, creates a vortex magnetic field.

Displacement current always occurs when the electric field changes over time. It can be in conductors, dielectrics, and vacuum. The full current density is equal to the sum of the conduction and displacement current densities:

(2.84)

Depending on the electrical conductivity of the medium and the rate of change of the field (frequency), terms in equation (2.84) play different roles. Suppose that the field strength changes according to the harmonic law, then the displacement current density: the conduction current density. The ratio of the maximum (amplitude) values of the conduction current density and displacement: For biological tissues at frequencies close to Hz, the amplitude values of these currents are of the same order. As the frequency of electromagnetic oscillations increases, the contribution of the bias current to the total current increases.

The passage of the bias current in different media is accompanied by the release of heat, which can be calculated according to the Joule-Lenz law (2.41):

(2.85)

If the field strength changes according to the harmonic law, that is

(2.86)

In the case of a homogeneous dielectric, the amount of heat can be calculated by the formula:

(2.87)

where is the angle between the intensity vector E and the polarization vector P, it is called the dielectric loss angle, and is some constant coefficient.